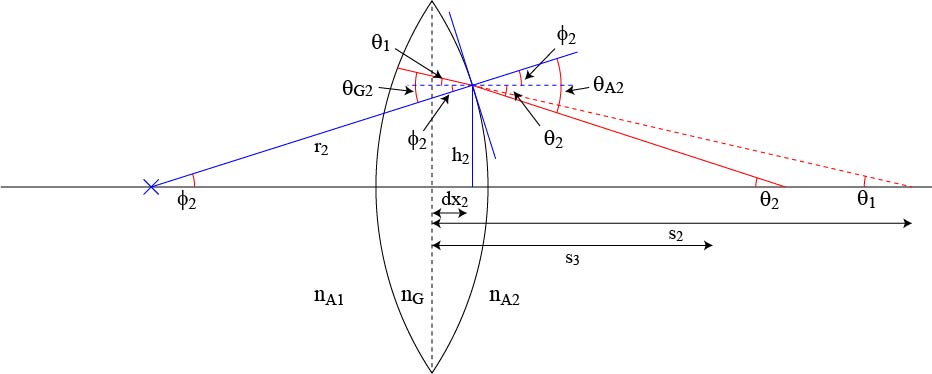
レンズ右側での屈折は,.

まずは,それぞれの記号の説明をしましょう.
φ2 : 光線がレンズ左側に当たった場所の曲率半径の軸に対する角度
r2 : 曲率回転半径
h2 : そのときの高さ
dx2 : そのときのレンズ中心からのずれ
θ1 : レンズ右側で屈折しない光線が軸と交わる点での角度
θ2 : レンズ右側で屈折した光線が軸と交わる点での角度
s2 : 屈折した光線が軸と交わる点の距離
θG2 : レンズからの入射角
θA2 : レンズ右側での屈折角
です.
幾何学的な関係は,
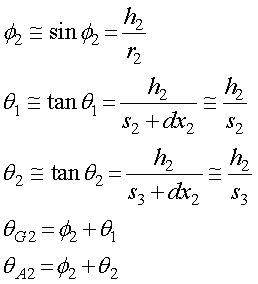
となります.
屈折の関係から,
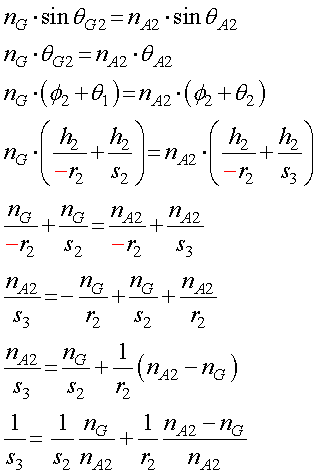
とs3を求めることができました.ここでもまたr2がマイナスの符号となっていることに注意してください.
次に,s2に前ページで導出した式を代入して,
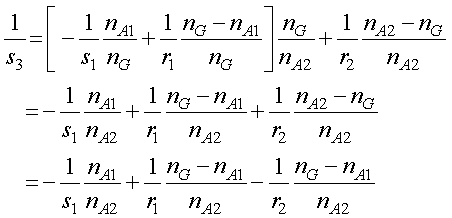
を得ることができます.
もし,入射光が平行光なら,s1,が無限大となるので,右辺第一項が0となり,さらに,A1,A2が空気なら,nA1=nA2=1,となるので,
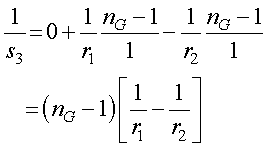
と,ここ,で求めた式と一致します.